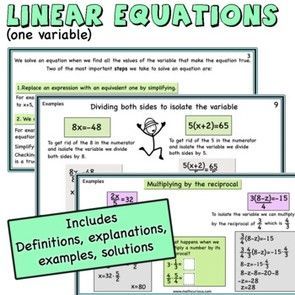
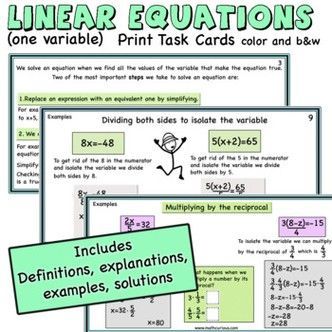
Algebra-Simplifying Expressions, Solving Linear Equations and Inequalities

May 27, 2022

I love teaching algebra especially in grades 5 and 6 when students start to learn about variables, expressions, and equations. Although algebra might seem strange to them at first, as they start to understand the rules they begin to enjoy this new chapter in their math adventures.

I cannot stress enough how important it is for students to be fully equipped and prepared before they dive into algebra. Make sure that your students are fluent with

basic math skills such as adding, subtracting, multiplying, and dividing
fractions, decimals, percents, their operations, and how they’re all related
the order of operations
Integers, the number line, and integer operations
Probability
Geometry formulas and vocabulary: perimeter, area, circumference, etc.
Ratio and proportion
exponents and their operations

I believe that the misconception that algebra is hard starts when students are not ready to tackle algebra just yet.

Starting with Algebra

By combining variables with numbers using mathematical operations we form mathematical expressions. A variable is a letter used to stand for a number. The letters most commonly used as variables are x, y, z, a, b, c, m, and n. The letters e and i have special values in algebra and are usually not used as variables. The letter o is usually not used because it can be mistaken for 0 (zero). Below are some examples of expressions.

4-7+5 2x+1 3x²+x-5 5(x-4)

Terms coefficients, and constant terms

A term is a product of a number and a variable raised to a power. The number in a term is the coefficient of the power of the variable. For example, in the expression picture of 3x²+2x-5 the terms are 3x², 2x, and 5. The coefficient of x² is 3 and the coefficient of x is 2. A term that is a number by itself is called a constant or a constant term.

Simplifying Expressions

As students start with pre-algebra it is important to understand how variables work and the concept of equivalence between two expressions. To find the value of the variable using two equivalent expressions we often need to simplify one or both the expressions. To simplify an expression means to write it as an equivalent expression with as few terms as possible, and write each term as simply as possible.

For example, the expression 2z+7-3z+4 can be simplified to -z+11, and the expression 4(z-6) +3 can be simplified to 4z² -12z+3.

We can write expressions for word problems to express the relations between the terms.

Example

Solving Linear Equations

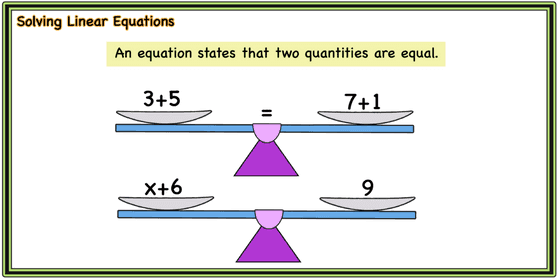
Two expressions are equivalent if they are equal for every value of the variable. An equation is true only for some values of the variable. The solutions to an equation are the values of the variable that make the equation true.

For example, the equation x+4=9 is true only for x=5

We solve an equation we find all the values of the variable that make the equation true. Two of the most important steps we take to solve an equation are:

Replace an expression with an equivalent one by simplifying. For example, for the equation 6x-5x+5=16 we can simplify the left-hand side
to x+5, so the equation becomes x+5=16

2. Perform the same mathematical operation on both sides of the equation. For example, starting with the equation x+5, we can subtract 5 from both sides of the equation to get x+5-5=16-5 Simplifying both sides of the equation gives us the solution of the equation which is x=11. Checking with the original equation we see that the equation is true for x=11

Isolating the variable

When we solve equations with one variable by performing operations on both sides of the equation and then simplifying the expressions until the variable is alone on one side of the equation we say that we isolate the variable.

For example

4z+2z-10=26
4z+2z-10+10=26+10
6z=36 z=6

(to isolate the variable we need to remove -10 from the left-hand side.
By adding 10 we cancel them out. Of course, we need to add 10 to the
right-hand side as well to keep the equivalence.)

Linear equations are equations in which every term is a constant term or a constant times the first power of the variable. 2z+3=5z-4 and a/2+1=7 are linear equations. x² +1=17 and 2/(a³-1)=56 are not linear equations.

Multiplying by the reciprocal

When a term or an expression is multiplied by a fraction, we can multiply both sides by the reciprocal of that fraction to eliminate the fraction. Multiplying a fraction by its reciprocal gives answer 1. example below

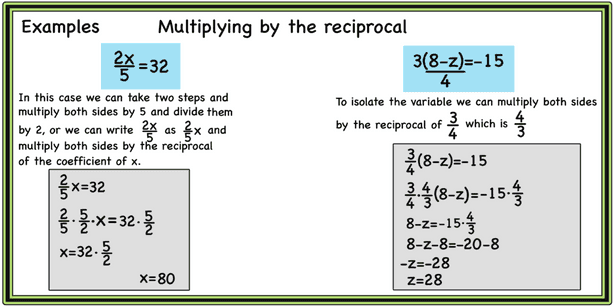
Eliminating the denominators

When one of the sides of the equation is divided by a term or an expression we can multiply both the sides with that term or expression to eliminate the denominators and simplify the equation.

For example,

Cross-multiplying

Rather than performing these multiplications as two separate steps, we can perform both at once. This process is called cross-multiplying.

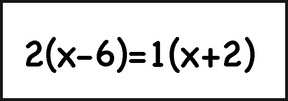
Variables on both sides of the equation

When the variable appears on both sides of the equation, we can use addition and subtraction to get all the terms with the variable on the same side. Similarly, we use addition and subtraction to get all the constant terms on the other side of the equation. In the example below we subtracted the variable term of the right side from both sides so that the variable will end up on the left side.

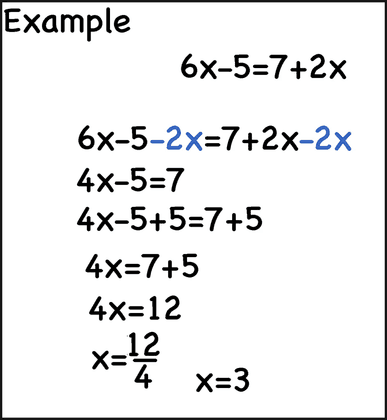
Using Equations to solve word problems

One of the best things about knowing algebra is that you can use variables and equations to easily solve tricky word problems. We can use equations to solve word problems. Once we decide which quantity the variable should represent we use the known information to find the value of the variable. When we find two different expressions that represent the same quantity we have an equation.

Example

Alice’s dog and Manny’s cat weigh 115 pounds together. Alice’s dog is 27 pounds heavier than Manny’s cat. How much does Alice’s dog weigh?

The unknown quantities are the weights of the dog and the cat so we can name one of these quantities x and use the information we have to calculate it. We need two expressions that represent the same quantity.

If we represent the weight of the dog with x then we have the equation x+(x-27)=115 We simplify the equation to 2x-27=115 2x=115+27 2×142 x=71

The dog’s weight is 71 pounds.

We could have represented the cat’s weight as x and used the equation x+(x+27)=115

Another example

Inequalities

When we know that an expression is greater than another, we can write an inequality to show the relationship between them. Inequalities can be strict or nonstrict. For example, x+6 > 4 and 6-2z < 8+z are strict inequalities and 2x-5 ≥ 9 and 5x+4 ≤ 8x-5 are nonstrict inequalities. Inequalities have more than one answer. The answer to an inequality is usually a range of numbers/values.

We can graph the values of the variable that satisfy the inequality on a number line. Example below.

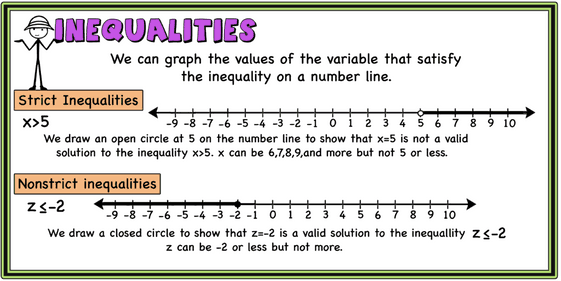
We can simplify and solve inequalities following the same steps as with equations. We can also use inequalities to solve word problems.

I have created 3 collections of resources for the concepts above (expressions, linear equations, and inequalities) (slides, print task cards, and worksheets) You can find the individual resources and the bundles below.

The resources include