Ratios, rates, and proportions along with conversion are concepts taught in middle school and they are a key part of algebra readiness. Simplifying ratios, finding equivalent ratios, finding unknown quantities, and solving word problems are some of the activities for practicing and understanding ratios. Before diving into ratios, rates, and proportions, students need to be fluent with their multiplication and division facts and understand fractions, equivalent fractions LCM, and GCF.
What are ratios?
In mathematics, a ratio is a way of expressing the relationship between two quantities. It is a comparison of two numbers by division. Ratios are used to compare, relate, and describe quantities and can be written as a fraction, a decimal, or a percentage.


Ratios can be used in a wide variety of contexts in mathematics, including geometry, finance, and statistics. In geometry, ratios are used to describe the relationship between the sides of a shape or the angles of a triangle. In finance, ratios are used to compare the financial performance of companies or to evaluate investments. In statistics, ratios are used to describe the relationship between two variables.
Equivalent Ratios-Ratios in Proportion
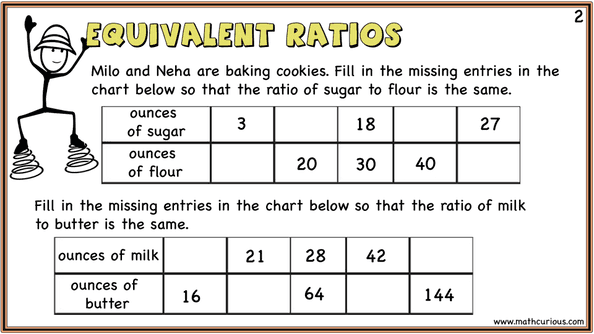
One important concept related to ratios is proportion. If two ratios are equivalent, they are said to be in proportion. For example, ratios 2:3 and 4:6 are in proportion because they can both be simplified to 2:3. This means that for every 2 units of the first quantity, there are 3 units of the second quantity, and the same is true for the second set of ratios.
Ratios can also be used to solve problems involving unknown quantities. For example, if we know that the ratio of the length to the width of a rectangle is 3:2, and we know that the length is 30 units, we can use the ratio to find the width by setting up a proportion:
length/width = 3/2 30/w = 3/2 w = 20
Therefore, the width of the rectangle is 20 units.
Ratios behave a lot like fractions. They are usually written in the simplest form as a ratio of positive integers with no common factor larger than one. Equivalent ratios can be written as equivalent fractions.
Multi-way ratios
Multi-way ratios refer to the comparison of three or more quantities, instead of just two. They are also known as compound ratios or joint ratios. Multi-way ratios are used in many areas of mathematics, including geometry, finance, and physics.
Multi-way ratios can be used to solve problems involving unknown quantities. For example, if we know that the ratio of the sides of a rectangular prism is 2:3:4, and we know that the volume of the prism is 240 cubic units, we can use the ratio to find the length, width, and height of the prism.
We can set up the following proportion to find the length of the prism:
2:3:4 = l:w:h 2x * 3x * 4x = 240 24x^3 = 240 x^3 = 10 x = ∛10
So the length is 2x = 2∛10 units, the width is 3x = 3∛10 units, and the height is 4x = 4∛10 units.


Proportions
Proportions are equations in which two ratios are set equal to each other. They are essentially, equivalent ratios expressed as fractions to compare two quantities or values. They express the relationship between one part of a whole and another part of the same whole. Proportions are used in many different areas, such as math, science, and finance, and are an important concept in everyday life.


Below you will find a collection of print and digital activities to teach ratios, rates, and proportions (google slides and print task cards) with explanations, examples, word problems, and other activities, (solutions included).
The resource includes 60 google slides or print task cards with solutions.


Find the google slides version here
Find the print task cards version here
Find the bundle with both the resources here
Find the worksheets version here- 13 worksheets + answer key




















