Multi-digit multiplication is considered one of the most “challenging” concepts to teach students. The reason for this view is, in my opinion, the fact that understanding multi-digit multiplication requires students to have gained a deep understanding of place value, and the multiplication properties. As the digits increase the process of solving a multi-digit multiplication problem becomes longer, with more steps to take. However, with activities that enable conceptual understanding and step-by-step practice, our students can all be successful.
While fluency and automaticity with the multiplication facts are great when practicing multi-digit multiplication students that haven’t mastered their multiplication facts can still learn multi-digit multiplication and use a multiplication table or any other helping tool. They might take more time to get the answers but they will be practicing and improving while understanding a new concept.
As I have mentioned above understanding place value before learning multi-digit multiplication is important. Practice modeling the numbers with base 10 blocks. Practice multiplying by 10, 100 and 1000 as well as their multiples. Take the time to practice each individually. Students should understand the place value rules before they use the “adding zeros” trick. For example, for the expression 32×100 the place value increases by two places since the ones are now 100s and the tens are now 1000s. Show it using base 10 blocks or other manipulatives. Be careful with “tricks” as when students don’t visualize the concept and understand they tend to get confused about them. A great way is to let the students “discover” the tricks themselves. The “adding zeros” trick can get confusing when division is introduced if students don’t have a conceptual understanding.
Another concept that needs to be well understood before diving into multi-digit multiplication is the distributive property of multiplication. Remind the students this property visually with arrays and explain how we can “break” numbers in the ones that are easier to multiply. The distributive property of multiplication is used in all the methods we use to teach multi-digit multiplication. The area model, or box method, or window method for example is a great way to show the distributive property. The algorithm of partial products is also the result of the distributive property.
Teaching/reminding the commutative and associative property of multiplication is important as well. We want our students to be flexible and be able to find the most efficient way of solving problems. We want them to discover strategies that will help them. Using the associative property will help them “break” a number in a different way. For example, 4×45 can be thought as 4x9x5 or better 4x5x9= 20×9=180 That’s where the commutative property comes in. Take time to discuss these properties with your students and you will be surprised at how much difference it will make. Solving problems mentally is as important as knowing the algorithms. It helps students strengthen their understanding and build useful strategies.
Once we have made sure that our students have a deep understanding of place value and the multiplication properties then we are clear to dive into multi-digit multiplication without regrets.
To enable our students to become flexible, efficient and successful mathematicians it is important to teach many methods. We need to ensure that every student is provided with many options. I believe that very different method we teach has something new to offer. I noticed that the area model method helps students to better understand the application of the distributive property. They carry that understanding to the algorithm. Students might select one method at first however once their understanding is strong they will comfortable trying other methods as well.
Area model
Before introducing the rectangle area model I like to start with arrays and discuss the distributive property of multiplication.
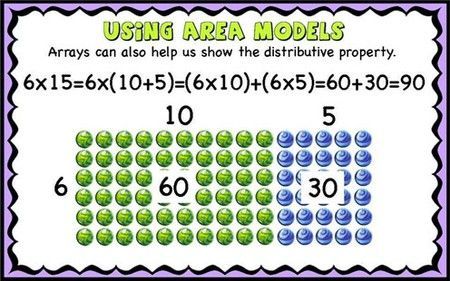
Then we move to the area model or box method. We model the multiplication problem as finding the area of a a rectangle. We use the distributive property and split the rectangle in smaller rectangles. We compute the areas of the rectangles and add them.
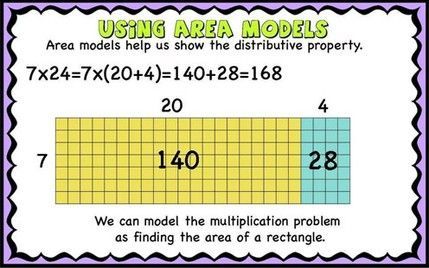
Next we move to the more simplified area model.

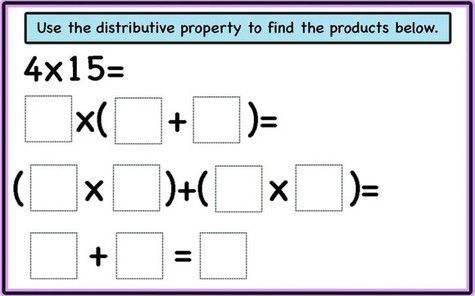
Another way of solving a multi-digit multiplication is the one below. Many students prefer this from the area model or move to this after the area model. It gets confusing as the numbers become longer but it is a great way for the students to show their understanding for 1×2 and 2×2 digit-multiplication.
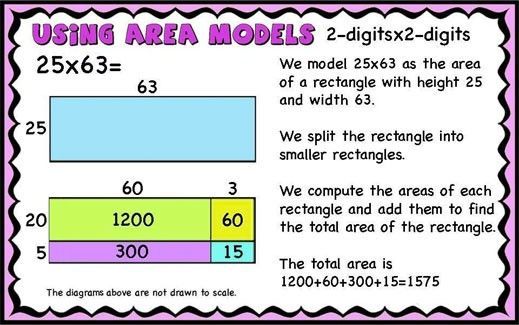
As we move to the 2×2 and 2×3 digit multiplication the area models become a little more complicated.
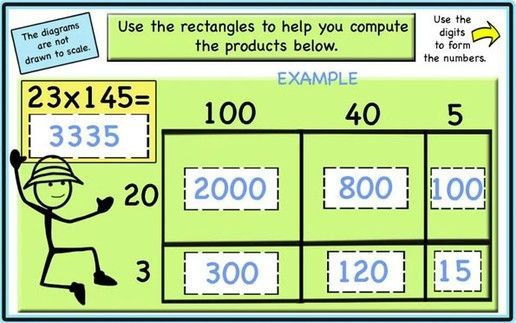
After area models, the students are ready to tackle the partial products algorithm. I prefer to start with the partial products algorithm and introduce the traditional one after a while as a more challenging method. I find that after mastering the partial products method the students understand the traditional algorithm better. I allow the students to use any method they like.
Partial Products Algorithm
According to this method we can stack the two numbers lining the ones and tens and use the distributive method to find the products. Then we add the products. Below is an example.

Here is another example

We have created a collection of print and digital (google slides) activities and worksheets to practice multi-digit multiplication. The unit includes
- Practicing 1×2, 1×3, 2×2, and 2×3-digit multiplication using the area models.
- Practicing 1×2, 1×3 2×2, and 2×3-digit multiplication using the partial products algorithm.
- Explanations, visuals, and examples
- Puzzles with the area model for 1×2, 1×3, 2×2, and 2×3-digit multiplication.
- Puzzles with the partial products algorithm for 1×2,1×3,2×2, and 2×3-digit multiplication.
- Mental math activities with multiplication tables and more.
- Multiplication Word problems
Below is a small sample
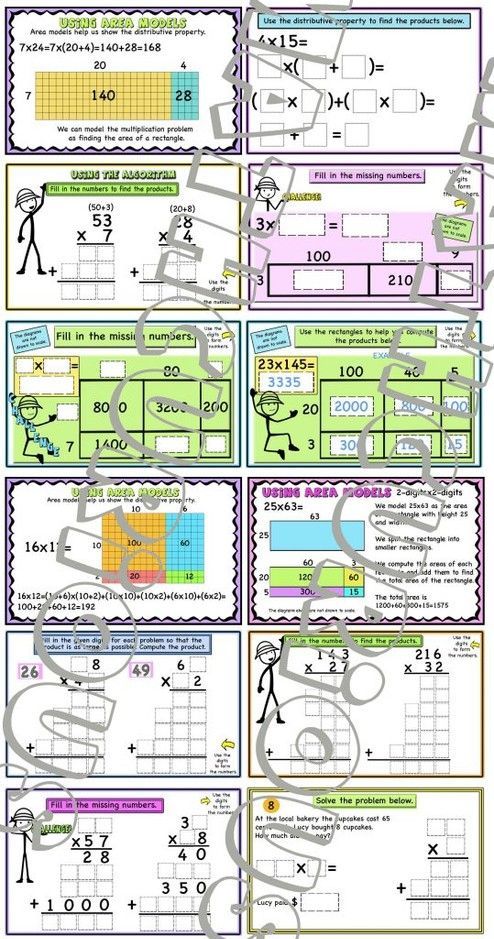

Find the free and premium version below.
Find the worksheets version of the resource here
Find the bundle with both the resources here
Check out our free latest 2-digit multiplication game


















