A strong conceptual understanding of division will help build students’ confidence and a strong foundation to base multi-digit division and division of decimals and fractions. The first step is to make sure that students understand what is division. Ask your students to explain what is division and find out what is their prior knowledge in order to target any misconceptions.
Give students objects to share among themselves or place in a number of groups and help them arrive at the conclusion that division is creating equal groups by fair Sharing. Most students will likely fair share the objects through one-to-one correspondence and engage in an early form of repeated subtraction. As the groups of objects become larger the students will begin to share more objects at a time. They realize that skip counting will help them solve the problem. At this point, they can also use number lines.
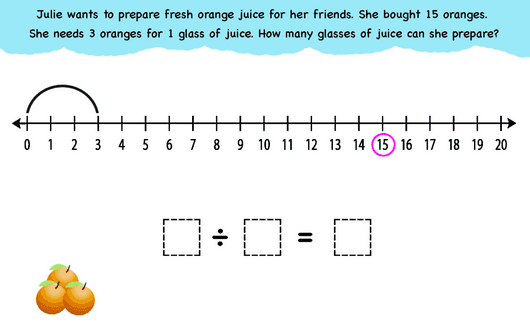
Types of division
There are two types of division and students should have the opportunity to experience problems of both kinds.
Partitive Division- Fair Share or Sharing Division
With Partitive Divison a problem requires the students to divide a group of items into a given number of groups. The number of items in each group is unknown. For example. “Farmer Joyce has 13 plants and wants to plant them in 3 rows. (three groups) How many plants will she plant in each row?” This is the type of division students intuitively experience when they first share a group of items with their classmates or share cookies with their siblings. Another example. Mr. James has baked 30 cupcakes. He is placing them evenly in 3 trays. how many cupcakes will he put in each tray? The number of groups is given and the number of items in each group is missing.
Quotative Division-Subtraction or Measurement Division
With quotative division, a problem requires the students to divide a group of items into smaller groups with the number of items in each group given. The number of groups is unknown. We can change the previous problems so they are Quotative Division examples. Farmer Joyce has 13 plants and wants to plant them in rows of 4. How many rows can she plant? Mr. James has baked 30 cupcakes. He is placing 10 cupcakes in each tray. How many trays does he need? The number of items in each group is given and the number of groups is missing.
It is important that students experience both types of division from the start so that when solving division problems without a story/word problem they can use both strategies.
For example, when solving the problem 24÷6 students can use the partitive division strategy and distribute 24 items in 6 groups or use the quotative division strategy and make groups of 6.
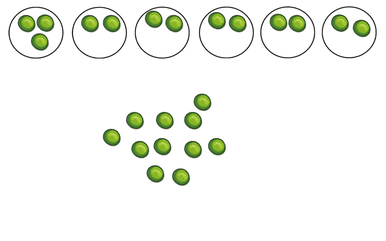

When students solve many types of word problems by creating their own diagrams they gain fluency and a deep understanding of division. Once they do they are ready to move on to arrays and relate division to multiplication facts.
Dividing with arrays
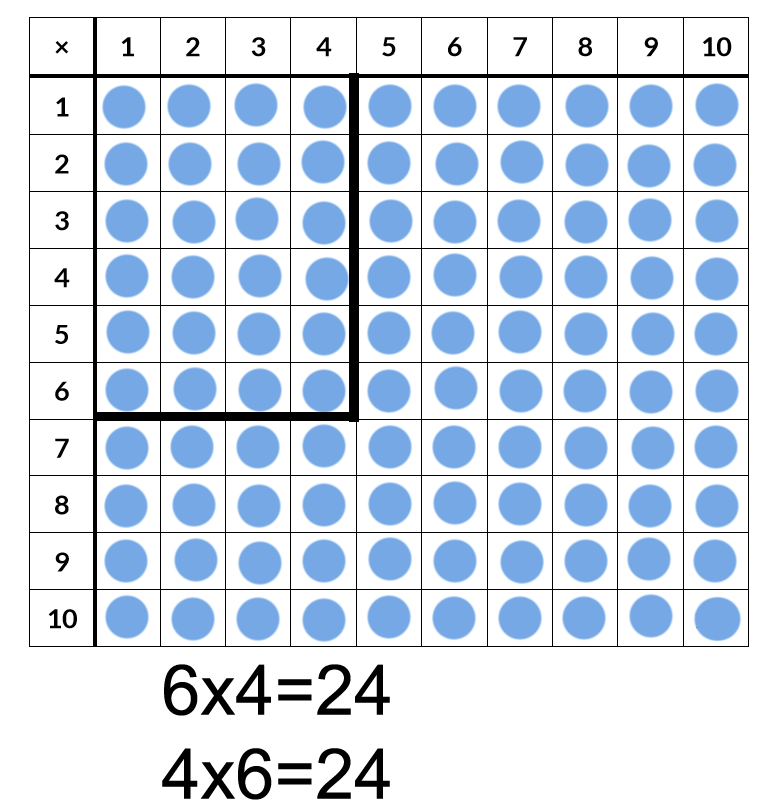
Organizing the items in rows and columns helps students see the problems as partitive and quotative division and visualize the solution. For example, for the problem 18÷3= the students can arrange the items in three rows (groups) or create rows of three. The array will look the same. This way they can relate division to area models and multiplication.
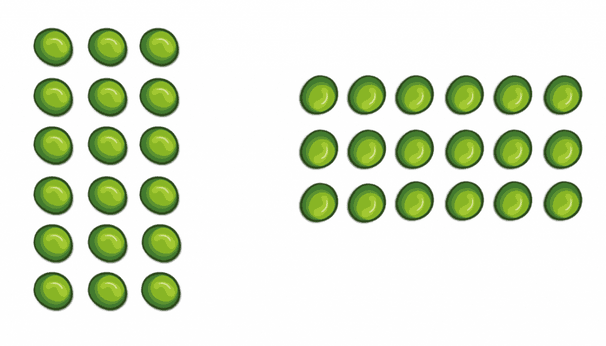
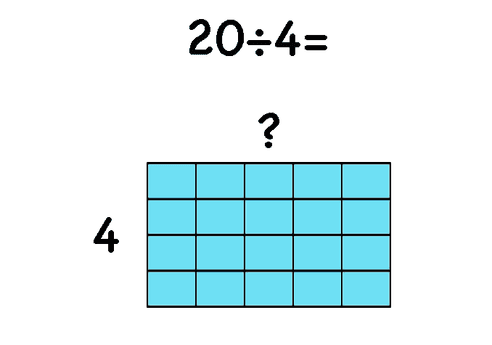
For example, the students can model the problem 20÷4= like this.
Once students have good practice with arrays and area models you can discuss how the multiplication table can help us with division. Start with the table as an area model and move on to the one with numbers.
Since division is the inverse operation of multiplication we can use the multiplication table to solve division problems, and the multiplication table becomes a division table. The students can use the table to help them find the closest multiple when solving division problems with remainders and more.
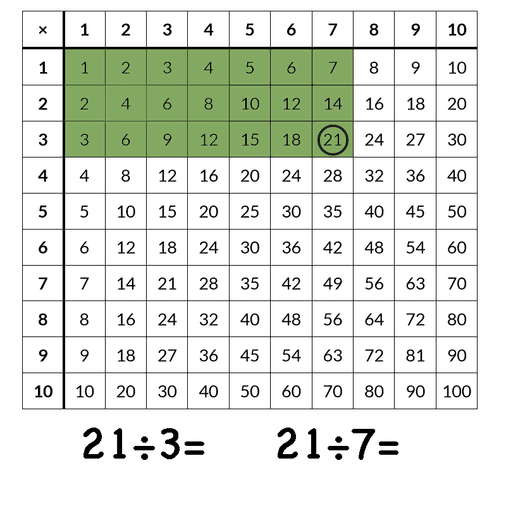
The table can help with remainders as well. Students can find the number closest to the dividend. For example for 58÷7= looking at the table of 7, they realize that 56 is the closest multiple of 7. Of course, if the students are fluent in multiplication facts they will be much faster with division problems as well. However, students that have not mastered their multiplication facts can still solve division problems and with good practice become fluent in both.
Distributive property in Division
Using the area models and the multiplication table you can also remind the students about the distributive property of multiplication and how it helps in division as well. For example, 72÷6= can be expressed as (60÷6)+(12÷6)= 12 We can split the array to “friendlier” numbers to solve the problem.
The same strategy can be applied for greater numbers as well. Before getting to the long division traditional algorithm or the partial quotients method you can solve problems using this strategy. It helps with mental math, shows how there are more than one ways to solve a problem and, prepares students for the algorithms. It is also a lot more fun as it encourages students to find relations and look at math problems as puzzles.
For example 167÷15= (150÷15) +(17÷15)= or (90+45+30+2)÷15= or (75+75+15+2)÷15
Using base 10 blocks for Division
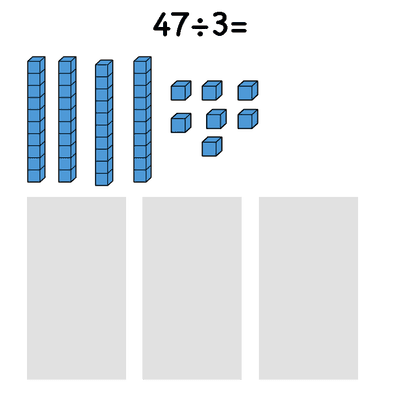
Base 10 blocks are very useful for dividing greater numbers and they prepare students for moving on to the algorithm.
For example, the problem 47÷3= can be solved like this.
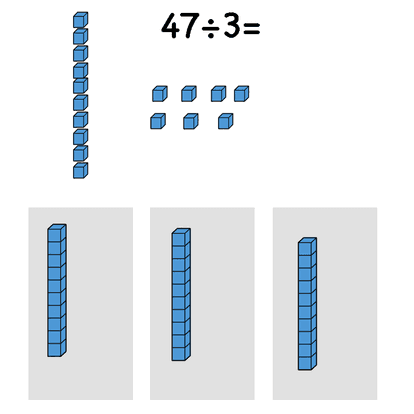
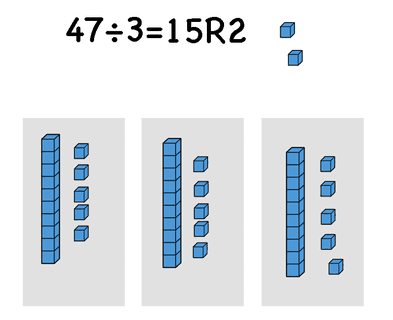
When you start with the algorithms of long division I recommend starting to explain it with base 10 blocks so that each step of the algorithm has meaning and students understand why it works. The distributive property is used here as well since I split the dividend to 30+15+2.
Learning Division Resources
We have prepared two jumbo collections of print and digital activity cards to help students practice division conceptually.
Diving into division – level 1

The first collection (level 1) is for the students that are just starting to learn division, grades 1,2,3 and it includes playful activities with lots of manipulatives to arrange and share in order to understand and solve division problems. (starting with dividing groups by two and moving on to arrays)
- Division vocabulary
- sharing equally
- partitive and quotative division
- word problems with manipulatives
- word problems with number-lines
- arrays (with and without remainder)
- matching expressions with arrangements/pictures
Below is a sample video
As always here is a free version for you. Free google slides version
Get the premium version here
The premium version includes 64 print activity cards and 78 google slides.
Diving into Division – Level 2
The second collection (level 2) is for grades 3,4,5 and it includes
- Division vocabulary
- partitive and quotative division
- word problems with number-lines
- word problems with arrays (with and without remainder)
- division with bars
- how to use the multiplication table for division
- how to solve division problems using base 10 blocks
- how to use friendlier numbers or partial quotients
- word problems using all strategies
Here is a sample
As always here is a free version for you. Free google slides version
Get the premium version here.
The premium version includes 92 print activity cards and 120 google slides.

















