Both educators and parents agree that fractions and their operations are one of the most difficult concepts for students to grasp. What makes fractions so challenging for students?
The introduction of the concept of fractions comes with a new vocabulary, new rules, new symbols, and a new concept of values between zero and 1. All this new information is hard to handle. However, when students are presented with visual simulations, activities, and examples from their everyday life they realize that fractions are all around them and they had been using them before learning about them. The vocabulary, the new symbols, and the rules become meaningful through hands-on activities and discussions.
There are a lot of rules concerning fractions and their operations and when students learn fractions as a series of rules they are much more likely to lose interest due to a lack of understanding. This is why is very important to help students gain a concrete understanding of the concept of fractions early on and avoid misconceptions. If misconceptions are not corrected in the beginning they make it difficult for students to understand more advanced concepts such as comparing fractions and operations of fractions.
Below are some common mistakes/misconceptions that students make. Being aware of these possible misconceptions helps us create activities that will help students gain a concrete and clear understanding of fractions.
Introducing Fractions-Parts and Wholes
It is important to help students construct the idea of fractional parts of the whole (for the area model of a fraction) and realize that a fraction is a part of a whole divided into equal parts. Students need to practice partitioning a variety of shapes into an equal number of parts. There is often a misconception that counting the number of parts of the shape instantly gives them the denominator.
For example, the shapes below are not all equally partitioned so the colored part of all them cannot be called 1/5. Only the first shape shows 1/5.
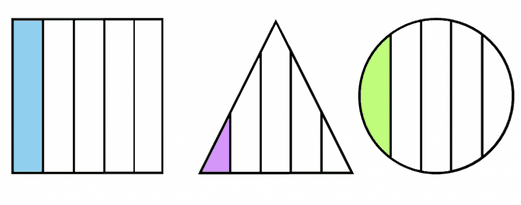
When it comes to number lines, the same misconception appears as many students often do not correctly partition the linear space relative to the fraction being shown.
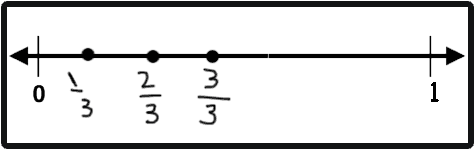
Showing many right and wrong examples as well as encouraging the students to partition the shapes themselves will help clear this misconception.
Often students do not recognize a fraction when fractional parts are separated by space. Presenting examples and providing different kinds of manipulatives to create different types of groups is recommended.

Moreover, students often need guidance to understand that the fractional part always depends on the whole. When students practice fractions with circles/discs they get used to the third blue shape below representing 1/4 and in their minds that particular shape becomes 1/4. However, if the first red shape becomes the whole then the same shape that represented 1/4 now represents 1/2.
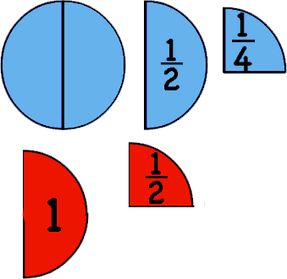
When working with tools such as Cuisenaire rods try using different sizes of rods as a whole. Fraction circles that don’t have the fraction marked on them can also be used to clear this misconception.

Students often do not recognize a fraction when the fractional parts are not all the same shape. For example, the colored part of the shape below is not recognized as 1/4. Showing more examples of area models of fractions where the parts are not all the same shape will help students understand.

Students might misidentify fractions of a set due to confusion with the area model as they expect all objects in a group to be the same. For example, in the group below students find it difficult to accept that the jelly bean is 1/4 of the candy because it is different.
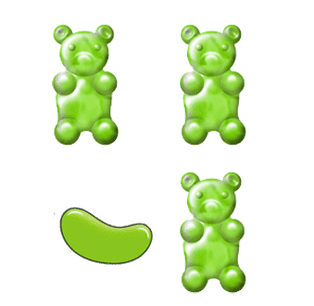
Here are some ides of activities you can do when introducing fractions.
- Ask students to show fractions using lego bricks.
- Use coins to show parts of 1 dollar.
- Cut fruits for a fruit salad.
- study a simple recipe and measure the ingredients.
- use play dough to create objects that you can “cut” into different parts.
- Use Cuisenaire rods to show parts of different wholes.
- Make paper plate fractions.
We have created some print and digital activity cards that will help students practice fractions (level1). There is a small sample of the slides below to have a look at.
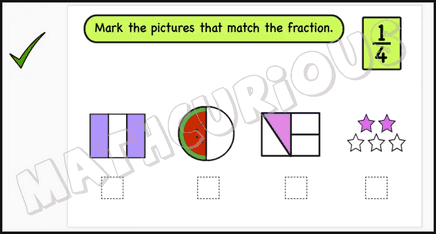
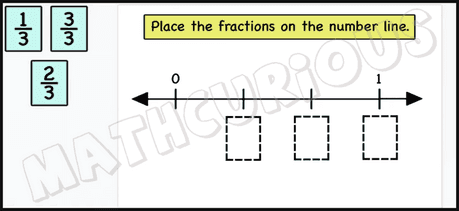

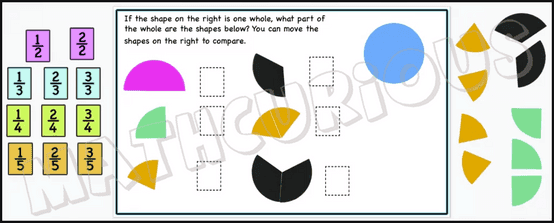
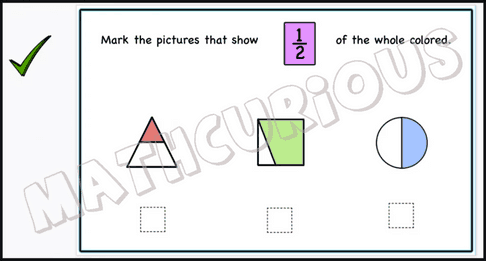

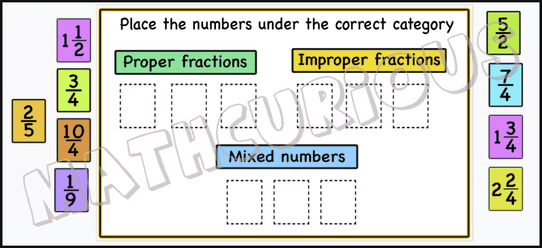
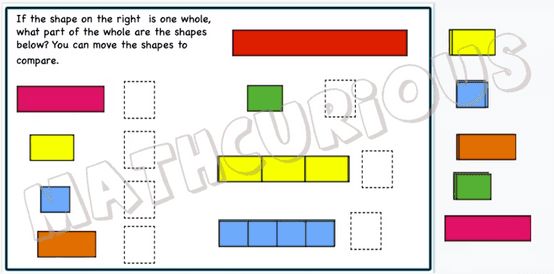
This resource includes 77 print and 80 digital activity cards to practice
- recognizing fractions as part of a shape
- recognizing fractions as part of a set
- partitioning into equal parts, groups
- Comparing parts to the whole
- Complete 1
- word form
- Introducing addition and subtraction of proper like fractions
- Introducing equivalence
The resource includes 77 print activity cards and 80 google slides activity cards.
Get the introducing fractions resource here here
How to use the activity cards.
You can use the activity cards for exploration and discussion, warm-ups, practice in groups, pairs or individual practice, homework, or assessment. The print cards can be used with manipulatives like rods, tiles, or discs. Provide objects for the students to use when working with fractions of groups.










