The division of fractions is often a challenging concept for students. Providing visual explanations and activities that include visuals helps them grasp the meaning of the division of fractions and gain a deep understanding. Keep in mind that before starting with the division of fractions students must have a concrete understanding of fractions as part of a whole, improper fractions and mixed numbers, equivalent fractions, like and unlike fractions, addition, and subtraction of like and unlike fractions.
When dividing fractions as well as when dividing whole numbers we use two techniques/interpretations. The measurement and the partitive technique.
In the measurement technique, we try to see how many times the divisor fits into the dividend. For example, for the question 18÷6 we will think “How many times 6 fits into 18, or how many groups of 6 fit into 18? We can add or take away a group of 6 at a time.

In the partitive technique, we solve for the one. For example, for the problem 18÷6 we will think “If 18 is divided into 6 groups, how much will be in one group?
Similarly, when dividing fractions we can use these two techniques.
Here is an example of the measurement technique of dividing fractions. With this method, both fractions are shown as part of the same whole.
Problem: I have 4/8 of a pizza left. If my friends and I take 1/8 each, how many friends can have pizza?
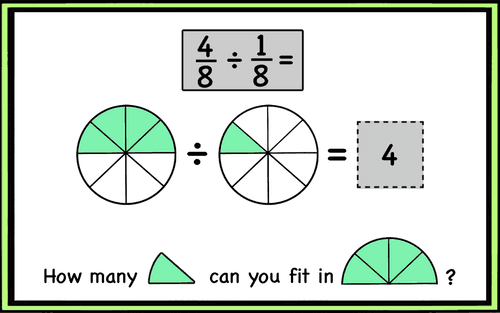
Different denominators
Students learn that to add or subtract fractions with different denominators they need to find the LCM and turn them into like fractions (with the same denominators) so that they show part of the same whole. Following the same method when dividing fractions with the measurement method helps them see both fractions as part of the same whole and figure out how many times the divisor fits in the dividend. Example below
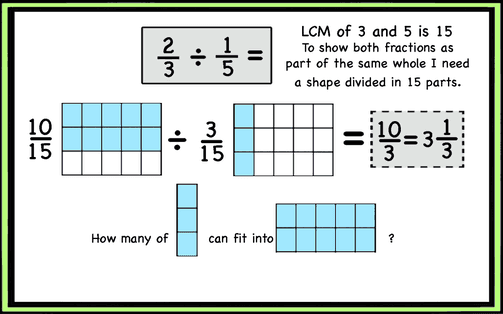
Partitive technique
Below is an example of the partitive technique of dividing fractions. With this method, I only show the first fraction and divide it based on the divisor.
Problem: 1/4 of a pound of blueberries costs 2/3 of a dollar. How many blueberries can I buy for 1$?
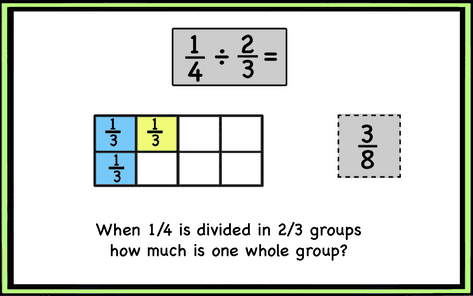
1/4 pound of blueberries cost 2/3 of a dollar. The shape shows the 1/4 pound of blueberries divided by 2 since it costs 2/3 of a dollar. This means that each of the two parts of the 1/4 pound of blueberries costs 1/3 a dollar. Therefore, with 1$ I can buy 3 parts. 3/8
The partitive technique is responsible for the algorithm that we all use. To divide a fraction by another fraction, multiply the first one by the reciprocal of the second one.
The partitive technique can explain why the algorithm works. 1/4 was multiplied by 1/2 (when we divide it into two pieces) and it became 1/8. Then multiplied by 3 it became 3/8
1/4÷2/3 = 1/4÷3/2 = 3/8
An algorithm is a series of steps that we follow to get to the answer. However, when these steps are followed blindly and don’t have any meaning for the students they tend to get confused and make mistakes. Mistakes such as “flipping” the first fraction or forgetting to “flip” the second fraction. Explaining visually why this algorithm works will help students understand and apply the algorithm correctly.
Dividing whole numbers by fractions and fractions by whole numbers visually also demonstrates how or why the algorithm works.
Below are some examples.
Dividing whole numbers by fractions.
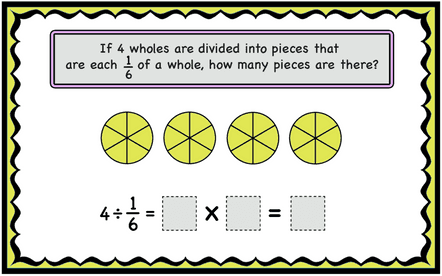
One whole has 6 pieces of 1/6, therefore, 4 wholes will have 4×6=24 pieces of 1/6. 4 is multiplied by the reciprocal of 1/6 which is 6. 4 can be shown as an improper fraction 4/1. 4/1×6/1=24 We multiply the first fraction (in this case 4) by the denominator of the second and divide by the numerator. We are actually multiplying with the reciprocal of 1/6.
Here is another example
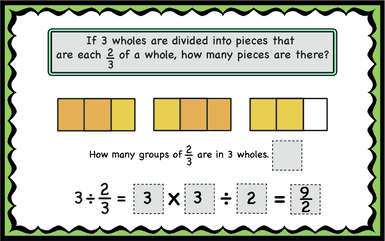
3 wholes have 3×3 1/3 so we have a total of 9/3. I am dividing by 2/3 which means that I need to put the thirds in groups of 2. 9/2=4 1/2 It is the same as multiplying 3×3/2 which is the reciprocal of 2/3.
Dividing fractions by whole numbers.
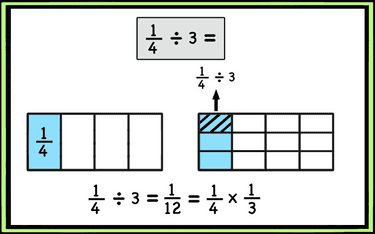
Dividing 1/4 by 3 is the same as finding 1/3 of 1/4 or multiplying 1/4×1/3 1/3 is the reciprocal of 3.
Once students solve many different problems, they will understand why and how the algorithm works and they will not make mistakes while applying it. Most importantly they will gain a deep understanding of the division of fractions.
I have created a collection of activity cards (print and digital) that you can use to practice the division of fractions. The activities are organized in the following order to help students gradually gain an understanding of the algorithm.
- Dividing whole numbers by fractions
- Dividing fractions by whole numbers
- Dividing like fractions
- Dividing unlike fractions
- Reciprocals and the algorithm
- Word problems
I focused on providing visuals and word problems for deeper understanding. I hope you find them useful.
The resource includes 52 print activity cards and 58 google slides to help practice the division of fractions.
Find the bundle with the multiplication and division of fractions print and digital activities here













