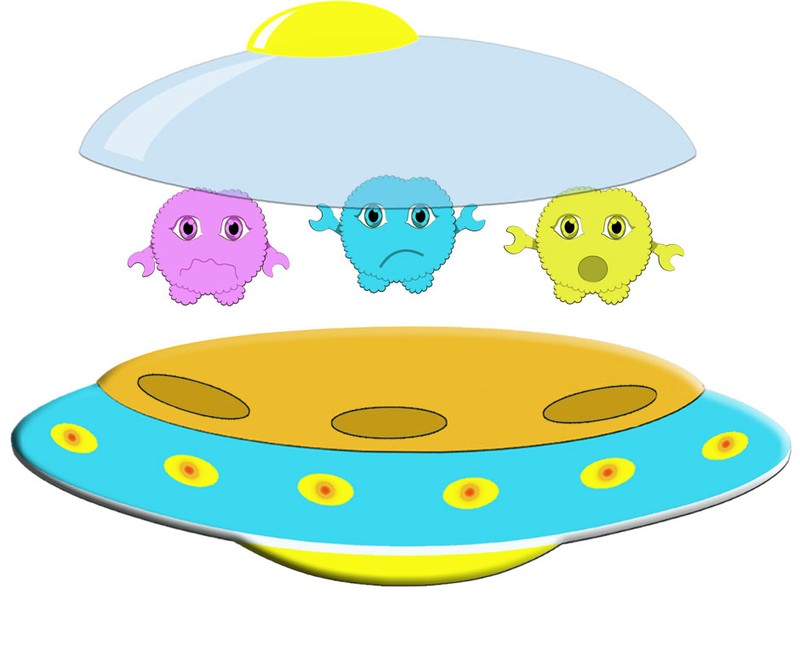
In how many different orders can the 3 Binions sit in their spaceship?
If the blue Binion sits in the first seat then there are two ways for the three Binions to sit.
If the purple Binion sits on the first seat there are two ways for the three Binions to sit.
If the yellow Binion takes the first seat then there are two ways for the three Binions to sit.
There is a total of 6 different ways for the Binions to sit in their spaceship.
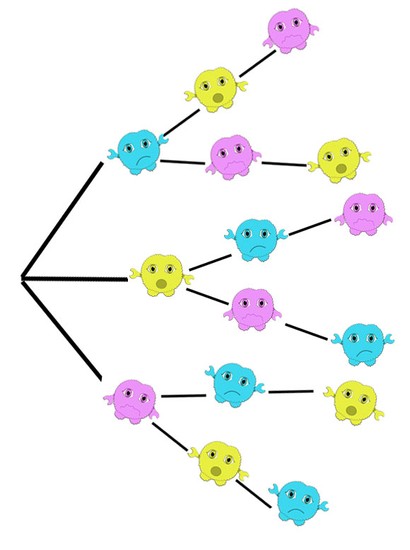
We can also solve this problem with a tree diagram.
There are 3 choices for the first seat, 2 choices for the second seat and 1 choice for the third seat.
3x2x1=6
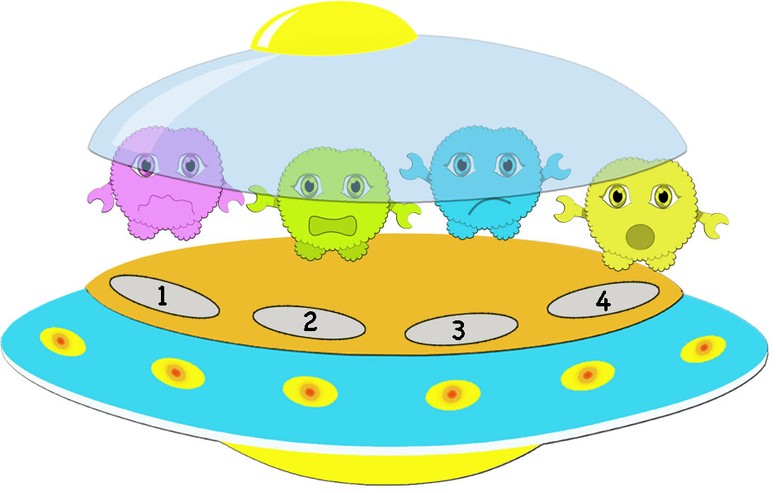
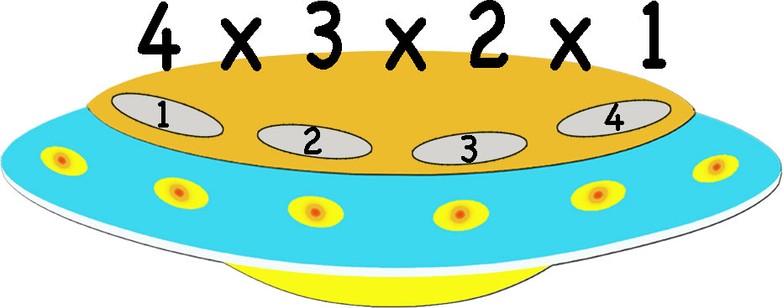
In how many different orders can the 4 Binions sit in the spaceship?
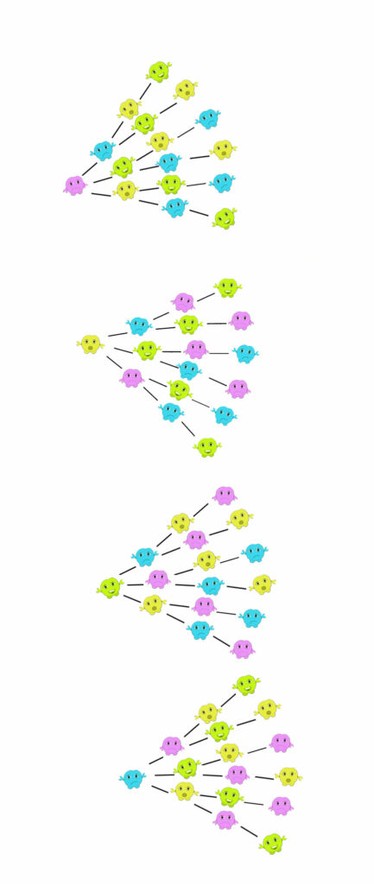
The tree diagram will look like this.
There are 4 choices for the first seat, 3 choices for the second seat, 2 choices for the third seat and 1 choice for the fourth seat.
So there are 24 different ways for the 4 Binions to sit in their spaceship.
There is a special shortcut for writing 4x3x2x1 and that is 4! (four factorial).
The exclamation point after the number tells us to multiply the number by each of the numbers below it all the way down to 1.
For example,
5!= 5x4x3x2x1= 120
6!= 6x5x4x3x2x1=720
The numbers grow very fast.
So how many different ways are there for 10 Binions to sit in order?
10!
10x9x8x7x6x5x4x3x2x1
When do we use factorial?
We use factorial when we need to find all the different ways of arranging a number of objects ( like aliens, people, numbers) in order.
Examples
1 . How many three-digit numbers can be made by arranging the digits 3, 5 and 8 in some order?
Answer
3!= 3x2x1=6
2 . In how many ways can John, Ally, Mary and Sanjay finish in order from 1st to 4th in the 100-yard race?
Answer
4! 4x3x2x1=24
3. In how many different ways can the letters in the word MATH be arranged. Use all the letters once.
4! = 4x3x2x1= 24
Here is a worksheet to practice factorial.