The Russian multiplication method is an interesting way of multiplying numbers by doubling and halving. Also called the Russian peasant multiplication, this algorithm allows students to multiply any two whole numbers. As I mentioned in the post about Ancient Egyptian Multiplication, teaching students alternative methods of solving problems helps them understand number relations better and shows them that there is more than one way to solve a problem.
How it works
Write the problem on the top and make a column under each of the numbers of the problem. Every time you half the number on the left and double the number on the right. when you need to half an odd number take out 1 so it is even and half it. We will talk about what remains in a minute.
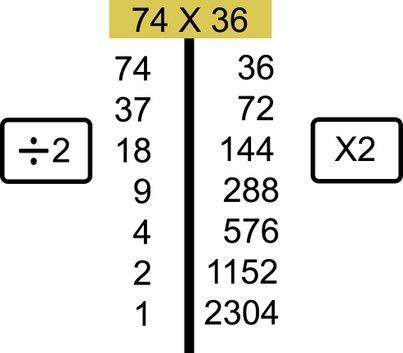
Next, cross out the rows in which the number on the left is even. Extend your line to cross out the corresponding number on the right as well.
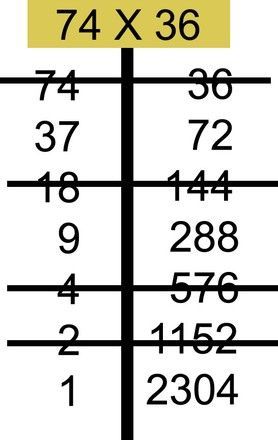
Find the sum of the remaining numbers in the right column. (the numbers in the right column that you did not strike through.) The sum of these numbers is equal to the product you would get from multiplying the original numbers using the standard method.
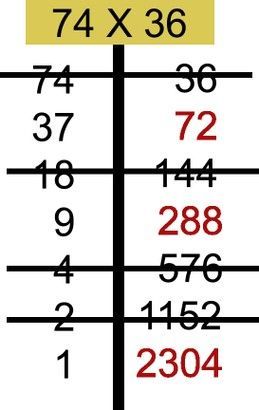
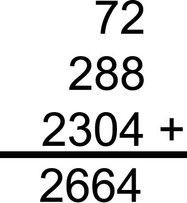
The Russian peasant multiplication method works because it converts the problem into binary (base 2) multiplication, rather than base 10. It does this by halving and doubling the numbers you are trying to multiply (since halving and doubling convert all numbers into multiples of 2, or into factors of numbers that are divisible by 2).
Ask your students why we had to add the two numbers 72 and 288. When we halved 37 we ignored the one to make the number even in order to divide it. That one we ignored was 1×72 so 72 needs to be added later. Same way when we halved 9 we ignored one to divide the even number. The one we ignored was 1×288 so 288 was added later.
What I personally like about the Russian multiplication method is that almost every step shows the equation in a different way. I believe that this helps the students figure out ways of doing calculations in their minds faster and more efficient. For example, 24×50= 12×100 which is easy to solve, or 25X50 = (12X100)+50
Thanks for visiting!
Please like and subscribe for more giveaways and updates.
Check out the rest of our free print to play games, task cards, worksheets, puzzles and more.
Check out our best selling games, now back in stock and available at amazon.com and amazon.ca
